Statistik

1. Grundlagen

1.1 Definition und Geschichte

Das Wort S. kommt von lateinisch statisticum, „den Staat betreffend“, bzw. italienisch statista, „der Staatsmann“, und bezeichnet die Wissenschaft von den Methoden und Verfahren zur Erfassung, Auswertung und Präsentation zahlenmäßiger Massendaten. Anfänge der S. reichen bis in die Antike zurück, als zu administrativen Zwecken Bevölkerungszahlen und Besitzverhältnisse erhoben wurden. Ein wichtiger neuzeitlicher Vorläufer der heutigen S. ist die im 17. Jh. aufkommende politische Arithmetik. Mit ihr begann das Zeitalter wissenschaftlich fundierter Bevölkerungsstudien und die Suche nach gesellschaftlich relevanten Regelmäßigkeiten. Eine andere W…urzel moderner S. ist die sog.e Universitäts-S., die ihre Aufgabe darin sah, „Staatsmerkwürdigkeiten“ sowie „Land und Leute“ (Wirtschaft, Lebensgewohnheiten, Sitten) zu beschreiben. Einen Schritt weiter ging der Sozialstatistiker Adolphe Quetelet, der in der von ihm begründeten „sozialen Physik“ im frühen 19. Jh. erstmals die Normalverteilung (Gauß’sche Glockenkurve) auf menschliche Eigenschaften und Verhaltensweisen bezog und daraus den Typus des „mittleren Menschen“ (homme moyen) entwickelte. Ohne die Wahrscheinlichkeitstheorie, die sich im 17. Jh. aus der Analyse von Glücksspielen zu entwickeln begann, ist die heutige wissenschaftliche S. nicht vorstellbar.

1.2 Wissenschaftliche Verortung der Statistik

S. ist ein für moderne Gesellschaften unverzichtbares Instrument der Informationsgewinnung. In allen wichtigen Lebensbereichen (Wirtschaft, Politik, Bevölkerung, Gesundheit, Bildung, Siedlung und Wohnen, Umwelt u. a.) dient sie der gesellschaftlichen Orientierung, Problemanalyse, Ursachenforschung und der Unterstützung von Entscheidungsprozessen. S. ist zu einer der Schlüsseldisziplinen der Wissens- und Informationsgesellschaft geworden (Stichwort Big Data). Neben ihrer praktisch-politischen Relevanz hat S. eine kaum zu überschätzende Bedeutung für den wissenschaftlichen Erkenntnisgewinn. Alle empirischen Wissenschaften (Natur- und Sozialwissenschaften, Medizin, Psychologie und Teile der Geisteswissenschaften) benötigen statistische Verfahren und Modelle, um Informationen über die Wirklichkeit zur Überprüfung und Erweiterung theoretischen Wissens zu gewinnen. In diesem Sinne ist S. eine universell einsetzbare Hilfswissenschaft für eine Vielzahl von Substanzwissenschaften, die an der Klärung empirischer Fragen interessiert sind.

S. liegt eine bes. Art der Wirklichkeitsbetrachtung zugrunde; sie bietet Informationen zum Gegenstand, die nicht durch intuitive Inaugenscheinnahme einiger weniger Fälle, sondern nur durch rechnerische Analyse einer Vielzahl von Untersuchungsobjekten (Individuen, Organisationen, Zeitungsartikel usw.) verfügbar gemacht werden können. Statistische Erkenntnisse sind daher nicht auf die Besonderheiten von Einzelfällen ausgerichtet, sondern auf die Auffindung und zusammenfassende Beschreibung von Mustern in Massendaten. Derartige Muster können sich – möglichst allg. gesagt – auf Eigenschaften einzelner Merkmale (z. B. Einkommen), auf Zusammenhänge von Merkmalen (z. B. von Einkommen und Bildung), auf Gruppen von Merkmalsträgern (z. B. soziale Milieus) sowie auf die zeitliche Entwicklung von Sachverhalten beziehen. Die relevanten Informationen werden durch verschiedene Kennzahlen (z. B. Mittelwert) erfasst und dargestellt. Der Teilbereich der S., der sich mit der zusammenfassenden Charakterisierung von Massendaten beschäftigt, wird als deskriptive S. bezeichnet. Der zweite große Teilbereich, die Inferenz-S. bzw. schließende (oder induktive) S., befasst sich mit der Verallgemeinerbarkeit statistischer Ergebnisse von einer Teilgesamtheit (Stichprobe) auf die jeweilige Grundgesamtheit.

S. ist zwar eine transdisziplinäre Hilfswissenschaft, dennoch gibt es verschiedene Verfahren und Kennwerte, die auf spezielle Erkenntnisinteressen einzelner substanzwissenschaftlicher Disziplinen zugeschnitten sind (z. B. bei der genetischen Erblichkeitsschätzung). Zudem werden in den einzelnen Disziplinen, je nach ihren bes.n Fragestellungen, unterschiedliche Verfahren bevorzugt. Die nachfolgend angesprochenen Auswertungsmethoden sind von grundlegender Bedeutung sowie auf die typischen Erkenntnisinteressen der Sozialwissenschaften (Ökonomie, Politikwissenschaft und Soziologie) zugeschnitten.

1.3 Datengewinnung

Der statistischen Datenanalyse ist i. d. R. eine Phase der Datengewinnung vorgelagert, wobei zwischen Primär- und Sekundär-S. zu unterscheiden ist. Bei der Sekundär-S. wird bereits vorhandenes (z. B. amtliches oder betriebswirtschaftliches) Datenmaterial unabhängig vom urspr.en Verwendungszweck für eine erneute Analyse herangezogen. Demgegenüber wird bei der Primär-S. eine eigens geplante Datenerhebung durchgeführt (z. B. mit Hilfe eines Fragebogens), deren Inhalte sich an der jeweiligen Erkenntnisabsicht ausrichten.

Datenerhebung im statistischen Sinne ist als Messung relevanter Variablen (Merkmale, Eigenschaften) bei ausgewählten Merkmalsträgern zu verstehen. Eine Messung lässt sich dadurch charakterisieren, dass die zu beobachtende Variable (z. B. Einkommen oder politische Einstellung) angemessen durch Zahlen abgebildet wird, wobei sich die Angemessenheit nach dem Skalenniveau der jeweiligen Variablen richtet. Skalenniveaus unterscheiden sich nach ihrem Informationsgehalt. Den niedrigsten hat die Nominalskala, die lediglich die Unterscheidung zwischen „gleich“ und „ungleich“ kennt (z. B. einzelne Konfessionen bei der Variablen Religionszugehörigkeit). Lassen sich die Ausprägungen einer Variablen zudem in eine Rangfolge (z. B. größer/kleiner, besser/schlechter, mehr/weniger) bringen, spricht man von einer Ordinalskala (z. B. Schulnoten). Eine Intervallskala ist dadurch bestimmt, dass sich über die Rangfolge hinaus gleich große Werteintervalle angeben lassen (z. B. der Abstand zwischen IQ 90 und 100 ist genauso groß wie der Abstand zwischen IQ 100 und 110). Eine Ratioskala erfordert zusätzlich einen absoluten Nullpunkt, der eine Verhältnisbestimmung einzelner Messwerte erlaubt. So ist die Aussage sinnvoll, eine Person verdiene doppelt so viel wie eine andere, aber nicht, sie sei doppelt so intelligent (die Intelligenzmessung sieht keinen absoluten Nullpunkt vor). Bei der Verwendung statistischer Auswertungsverfahren ist grundsätzlich das Skalenniveau zu beachten. Viele bedeutsame, weit verbreitete Verfahren (z. B. Korrelation und Regression) setzen ein metrisches Skalenniveau (zumindest Intervallskala) voraus.

Datenerhebungen werden zumeist nicht als Vollerhebungen einer Grundgesamtheit (z. B. die gesamte Wohnbevölkerung eines Landes), sondern als Teilerhebungen durchgeführt. Wird die dazu nötige Auswahl von Merkmalsträgern (Stichprobe) mit Hilfe des Zufallsprinzips durchgeführt, liegt eine Zufallsstichprobe vor (jedes Element der Grundgesamtheit hat eine bestimmte Chance, in die Stichprobe zu gelangen). In diesem Zusammenhang wird etwas missverständlich auch von einer repräsentativen Stichprobe gesprochen. Damit ist ein verzerrungsfreies Abbild der Grundgesamtheit gemeint. In diesem Sinne können Zufallsstichproben allerdings keine Repräsentativität garantieren; ab einer gewissen Größe der Stichprobe ist es aber sehr unwahrscheinlich, dass grobe Verzerrungen auftreten. Verallgemeinerungen von einer Stichprobe auf die Grundgesamtheit sind statistisch nur dann begründet, wenn eine Zufallsstichprobe vorliegt. Aus mindestens zwei Gründen hat man es aber meist, zumindest in der sozialwissenschaftlichen Umfrageforschung (Demoskopie), nicht mit Zufallsstichproben zu tun. Erstens basiert schon das Auswahlverfahren häufig nicht auf dem Zufallsprinzip, etwa wenn Quotenstichproben gezogen werden (die Auswahl der Teilnehmer erfolgt nach Gutdünken, es müssen lediglich bestimmte Quoten, z. B. hinsichtlich des Alters oder Geschlechts, eingehalten werden). Ein Aufruf im Internet, an einer Befragung teilzunehmen, erfüllt ebenfalls nicht die Kriterien einer Zufallsstichprobe. Zweitens sind viele Personen nicht bereit, an einer Umfrage teilzunehmen, d. h. eine Zufallsstichprobe kann aufgrund von Ausfällen (Nonresponse) selbst dann nicht realisiert werden, wenn die vorausgegangene Auswahl der zu befragenden Personen zufällig erfolgte. Liegt keine Zufallsstichprobe vor, ist die Anwendung aller Methoden der schließenden S. fragwürdig und eigentlich unzulässig.

2. Univariate Datenanalyse

Die grundlegendste Form statistischen Auswertung ist die univariate (eindimensionale) Datenanalyse, bei der lediglich eine einzige Variable betrachtet wird. Eine Häufigkeitsverteilung wird erstellt, indem man auszählt, wie häufig die Ausprägungen einer Variablen (z. B. der jeweilige Familienstand) vorkommen. Das Resultat dieser Auszählung kann in absoluten Häufigkeiten angegeben werden, meist werden jedoch relative Häufigkeiten (bzw. Prozentsätze) ausgewiesen. So kann man z. B. angeben, wie groß die Bevölkerungsanteile sind, die ledig, verheiratet, geschieden oder verwitwet sind. Manche metrische Variablen (z. B. Körpergröße) sind stetig, d. h. sie können innerhalb eines bestimmten Bereiches jeden beliebigen Wert annehmen; für derartige Variablen lassen sich Häufigkeiten nur dann berechnen, wenn ihre Werte zuvor klassiert (in Intervalle eingeteilt) wurden. Häufigkeitsverteilungen werden entweder als Tabelle oder grafisch dargestellt, wobei je nach Skalenniveau verschiedene Diagrammformen zur Verfügung stehen (u. a. Balken- oder Kreisdiagramm, Histogramm).

Zur möglichst prägnanten Charakterisierung einer Häufigkeitsverteilung werden statistische Maßzahlen eingesetzt. Maße der zentralen Tendenz (Lagemaße) bilden „typische“ Verteilungswerte ab. Die am häufigsten auftretende Ausprägung einer Variablen wird als Modus bezeichnet. Der Median ist der mittlere Wert einer Verteilung; er teilt eine nach Größe geordnete Reihe von Messwerten genau in der Mitte auf. Der bekanntere Mittelwert ist das arithmetische Mittel, das sich aus der Summe aller Beobachtungswerte geteilt durch die Fallzahl ergibt. Die Berechnung des arithmetischen Mittels setzt ein metrisches Skalenniveau voraus, für den Median genügen bereits ordinale Daten. Median und arithmetisches Mittel müssen nicht übereinstimmen. So betrug in Deutschland 2014 das durchschnittliche Einkommen von Vollzeitarbeitnehmern 3.440 Euro, wohingegen sich das Medianeinkommen auf knapp 3.000 Euro belief. Beide Angaben sind korrekt, geben aber unterschiedliche Sichtweisen des „mittleren“ Einkommens wieder, welche mit verschiedenen Kommunikationsabsichten verbunden sein können (Hervorhebung eines „hohen“ v „niedrigen“ mittleren Einkommens).

Soll das durchschnittliche Wachstum einer Größe innerhalb eines Zeitraumes (z. B. Wirtschaftswachstum) berechnet werden, ist das arithmetische Mittel ungeeignet; stattdessen ist das geometrische Mittel einzusetzen. Es berechnet sich als n-te W…urzel aus dem Produkt von n Beobachtungswerten. Ist das durchschnittliche Wachstum einer Variablen bekannt, lässt sich die Verdoppelungszeit leicht mit Hilfe einer Daumenregel ermitteln (70 geteilt durch Wachstum in %): So verdoppelt sich die Weltbevölkerung etwa alle 35 Jahre, wenn sie um 2 % jährlich wächst.

Um die Schwankung bzw. Heterogenität von Messwerten zu erfassen, wird die Beschreibung von Verteilungen i. d. R. durch Streuungsmaße bzw. Dispersionsmaße ergänzt. Das wichtigste und am häufigsten verwendete Streuungsmaß ist die Varianz, die mittlere quadratische Abweichung der Einzelwerte von ihrem arithmetischen Mittel. Zur leichteren Interpretation zieht man aus der Kennzahl die Quadratwurzel und erhält so die Standardabweichung. Das einfachste, aber auch (bis auf Sonderfälle) am wenigsten aussagekräftige Streuungsmaß ist die Spannweite, die den Abstand zwischen dem größten und kleinsten Wert beschreibt. Der (grafisch darstellbare) Quartilsabstand misst den Abstand, den die mittleren 50 % einer Verteilung aufspannen. Alle genannten Streuungsmaße setzen Intervallskalenniveau voraus. Für nominal- und ordinalskalierte Merkmale stehen andere, teils komplexe Streuungsmaße zur Verfügung (Simpsons D, Herfindal-Index, Entropie). Unabhängig von speziellen Maßen ist bei nominalen Merkmalen die maximale Streuung erreicht, wenn alle Ausprägungen gleich verteilt sind; bei ordinalen Merkmalen ist das der Fall, wenn nur der niedrigste und der höchste Wert (mit gleicher Häufigkeit) besetzt sind. Minimal hingegen ist die Streuung, wenn alle Beobachtungen nur einen einzigen Wert annehmen. Dies gilt für Merkmale aller Skalenniveaus.

Ähnlich wie Streuungsmaße messen Konzentrationsmaße, wie gleich bzw. ungleich Merkmale verteilt sind. Zu den bekanntesten Konzentrationsmaßen zählt der Gini-Koeffizient. Er nimmt Werte zwischen 0 und 1 an und wird v. a. zur Messung der Einkommens- und Vermögensungleichheit eingesetzt. Ein Wert von 0 besagt, dass keinerlei Ungleichheit herrscht bzw. das Einkommen (Vermögen) aller Personen gleich ist. Im umgekehrten Fall, wenn nur eine einzige Person (oder eine einzige Klasse von Personen) das gesamte Einkommen (Vermögen) auf sich vereint, herrscht maximale Ungleichheit. Der Gini-Koeffizient nimmt dann den Wert 1 an. So lagen die Gini-Koeffizienten des Einkommens 2014 für die USA bei 0,39 und für Deutschland bei 0,29 (d. h. in Deutschland ist die Einkommensungleichheit etwas geringer).

3. Bivariate Datenanalyse

Das wichtigste Informationspotenzial der S. liegt nicht in der Beschreibung einzelner Merkmale, sondern in der Analyse von Merkmalszusammenhängen. Im einfachsten Fall wird der Zusammenhang zwischen zwei Variablen untersucht (bivariate Datenanalyse), etwa der zwischen Bildungsabschluss und Parteipräferenz. Ausgangspunkt der bivariaten Datenanalyse ist häufig (insb. bei nominalen und ordinalen Variablen) eine Kreuztabelle, in der die gemeinsame (bivariate) Häufigkeitsverteilung eingetragen wird. Diese ergibt sich aus den Häufigkeiten aller Merkmalskombinationen der beiden beteiligten Variablen. Wie bei der univariaten stehen auch bei der bivariaten Datenanalyse verschiedene Maßzahlen (hier zur Messung von Zusammenhängen) zur Verfügung, deren Anwendbarkeit und Interpretationsmöglichkeiten wiederum vom Skalenniveau der betreffenden Variablen abhängt (s. Tab. 1).

Skalenniveau	Statistische Zusammenhangsmaße	Informationsgehalt über den Zusammenhang
Nominal	Prozentsatzdifferenz, Phi, Cramers V	Stärke
Ordinal	Taub, Gamma, Rangkorrelation	Stärke, Richtung
Metrisch	Pearsons r	Stärke, Richtung, Form

Tab. 1: Ausgewählte Zusammenhangsmaße

Unabhängig vom Skalenniveau lässt sich die Stärke eines Zusammenhangs ermitteln. Die S. ist bestrebt, Maße so zu normieren, dass sie den Wert 0 bei Zusammenhangslosigkeit und den Wert 1 (dem Betrag nach) annehmen, wenn zwei Variablen perfekt zusammenhängen. Eines der einfachsten Zusammenhangsmaße für zwei nominale Variablen (mit nur je zwei Ausprägungen) ist die Prozentsatzdifferenz. Ist z. B. der prozentuale Anteil von Frauen und Männern, die einen Migrationshintergrund haben, gleich groß, besteht kein Zusammenhang zwischen den Variablen Geschlecht und Migrationshintergrund. Je mehr die geschlechtsspezifischen Prozentsätze (bedingte relative Verteilungen) allerdings voneinander abweichen, desto stärker ist der Zusammenhang. Ein anderes, voraussetzungsvolleres Zusammenhangsmaß für nominale Variablen mit zwei Ausprägungen ist Phi. Liegen mehr als zwei Ausprägungen vor, steht u. a. Cramers V zur Verfügung. Bei ordinalskalierten Variablen kann nicht nur die Stärke, sondern auch die Richtung eines Zusammenhangs interpretiert werden. Die gebräuchlichsten Maße sind die Konkordanzmaße Tau_b und Gamma. Ihr Wertebereich liegt zwischen –1 und 1, wobei positive Werte auf einen positiven Zusammenhang (größere Werte der Variablen X gehen mit größeren Werte der Variablen Y einher) und negative Werte auf einen negativen Zusammenhang hinweisen (größere Werte der Variablen X gehen mit kleineren Werten der Variablen Y einher und umgekehrt). Ein weiteres gebräuchliches ordinales Zusammenhangsmaß ist die Rangkorrelation nach Charles Edward Spearman (sie misst die Ähnlichkeit zweier Rangordnungen).

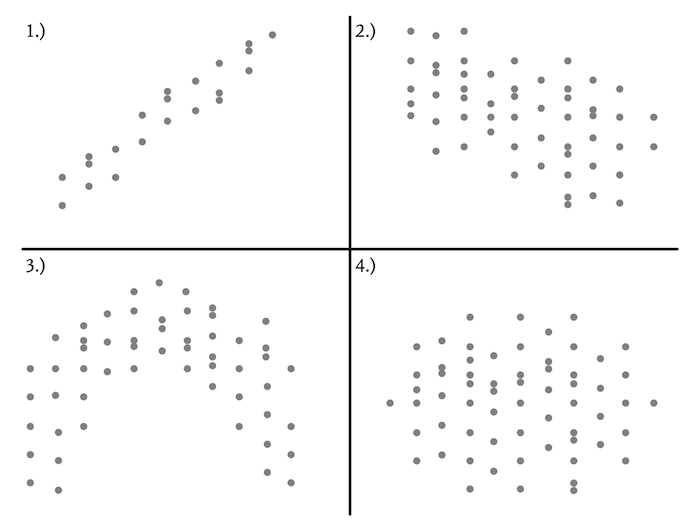
Zusammenhänge zwischen zwei metrischen Variablen (z. B. Anzahl der Schuljahre und Einkommen) lassen sich in Streudiagrammen darstellen (idealisierte Auswahl: Abb. 1).

Abb. 1: Ausgewählte (idealisierte) Zusammenhänge metrischer Merkmale im Streudiagramm

Diese Zusammenhänge können nach Stärke, Richtung und (funktionaler) Form unterschieden werden. Im ersten Diagramm ist ein stark positiver und im zweiten ein schwach negativer – jeweils linearer – Zusammenhang zu sehen; das dritte Diagramm bildet einen nichtlinearen (umgekehrt u-förmigen) Zusammenhang ab und im vierten Diagramm herrscht statistische Unabhängigkeit (kein Zusammenhang). Zur numerischen Beschreibung linearer Zusammenhänge wird der Korrelationskoeffizient r (Pearsons r) eingesetzt. Er wird 1 (vollständig positiver Zusammenhang), wenn alle Wertepaare zweier Variablen (Punkte im Streudiagramm) exakt auf einer von links nach rechts ansteigenden Geraden liegen; sind umgekehrt alle Wertepaare auf einer fallenden Linie angeordnet, nimmt er den Wert –1 an (vollständig negativer Zusammenhang). Je näher der Wert von r bei 0 liegt, desto geringer ist der lineare Zusammenhang. Dieser kann auch als Funktion einer unabhängigen (erklärenden) Variablen X und abhängigen Variablen Y in Gestalt einer Regressionsgeraden ausgedrückt werden: Y = b₀ + b₁*x_i. Die beiden Parameter b₀ und b₁ werden so gewählt, dass die Regressionsgerade optimal in der Punktewolke eines Streudiagramms liegt (Methode der kleinsten Quadrate: die Summe der quadrierten Abstände von Punkten und Gerade ist minimal).

4. Multivariate Datenanalyse

4.1 Regressionsanalytische Verfahren

Obwohl bereits bivariate Analysen häufig bedeutsame Einblicke in Sachzusammenhänge eröffnen, bietet die in den letzten Jahrzehnten erheblich weiterentwickelte multivariate (viele Variablen berücksichtigende) S. völlig neue Erkenntnismöglichkeiten. Dies trifft insb. auf die Ursachenforschung zu, bei der es in den Sozialwissenschaften darum geht, soziale bzw. ökonomische Phänomene zu erklären. In der statistischen Analyse wird von „unabhängiger Variable“ statt von „Ursache“ und von „abhängiger Variable“ statt von „Wirkung“ gesprochen. Ein Grundproblem statistischer Ursachenforschung liegt darin, dass von einem Zusammenhang nicht zwangsläufig auf Kausalität (Ursache-Wirkungs-Beziehung) geschlossen werden kann. So gibt es einen statistischen Zusammenhang zwischen Einkommen und der Häufigkeit hochkultureller Aktivitäten (Besuch von Oper, Theater, Museen etc.); ob die Höhe des Einkommens aber auch Ursache solcher Aktivitäten ist, bleibt offen. Möglicherweise ist die Bildung eine relevante unabhängige Variable (Drittvariable), die sowohl das Einkommen als auch das hochkulturelle Interesse beeinflusst.

Ein grundlegendes statistisches Verfahren zur kausalanalytischen Überprüfung möglicher Einflussfaktoren ist die multiple Regressionsanalyse. In Erweiterung der bivariaten Regression kann sie wie folgt formuliert werden: Y = b₀ + b₁*x₁ +…+ b_n*x_n. Alle Variablen müssen metrisches Skalenniveau aufweisen. Maßgeblich für die Interpretation sind die Regressionsgewichte von b₁ bis b_n. Sie geben Ausmaß und Richtung der durchschnittlichen Veränderung von Y (z. B. erhöhte hochkulturelle Aktivität) an, wenn die jeweilige erklärende Variable um eine Einheit (z. B. 1 Euro höheres Einkommen) verändert wird. Dabei ist zu berücksichtigen, dass alle anderen Variablen statistisch konstant gehalten und somit kontrolliert werden. In diesem Sinne ist jeder an den Regressionsgewichten zu bemessende Einfluss einer unabhängigen Variablen auf Y als bereinigter (partieller) Effekt zu werten. In diesem Kontext wird auch von Drittvariablenkontrolle gesprochen. Geht der bereinigte Effekt nach Kontrolle relevanter Drittvariablen gegen null (z. B. beim Einkommen), muss man davon ausgehen, dass die betreffende Variable keinen kausalen Effekt auf die abhängige Variable Y hat. Bleibt jedoch ein substanzieller bereinigter Effekt erhalten, ist möglicherweise ein kausaler Effekt vorhanden. Allerdings könnten weitere, unbeobachtete Drittvariablen von Bedeutung sein. Kausalität lässt sich daher selbst mit komplexen statistischen Verfahren nicht beweisen; man kann lediglich mögliche Alternativen ausschließen.

Regressionsanalyse ist heute ein Obergriff für eine Vielfalt von Verfahren, Varianten und Auswertungsstrategien. So gibt es Verfahren, die statistische Einflüsse auf dichotome (zweiwertige) und nominale abhängige Variablen mit mehreren Ausprägungen analysieren können (logistische und multinomiale Regression). Unter Mehrebenenanalysen sind Regressionsmodelle zu verstehen, die hierarchische Datenstrukturen berücksichtigen. Solche Strukturen entstehen, wenn nicht nur Individualdaten (z. B. persönliche Leistungsbereitschaft), sondern auch Gruppendaten einer höheren Ebene (z. B. Arbeitsklima) in die Analyse eingehen. Pfadanalysen verketten Variablen zu kausalen Pfaden, auf denen sich über mehrere „Stationen“ hinweg die Einflüsse unabhängiger Variablen auf die abhängige Variable nachverfolgen lassen. Auch bei der Analyse zeitbezogener Daten spielen Regressionsverfahren eine zentrale Rolle.

4.2 Dimensionsanalytische Verfahren

Die Faktorenanalyse ist ein gängiges multivariates Verfahren mit einer anderen typischen Zielsetzung. Mit ihrer Hilfe lässt sich eine Vielzahl von Variablen zu möglichst wenigen, jeweils voneinander unabhängigen Hintergrunddimensionen bündeln. Werden z. B. in einer Umfrage bei jeder Person dutzende von Variablen zu Musik-, Literatur-, Fernseh- und Freizeitpräferenzen erhoben, kann man diesen vieldimensionalen Variablenraum nach grundlegenden kulturellen Orientierungsdimensionen durchforsten. Die explorative Identifikation einzelner Dimensionen kann man sich so vorstellen, dass die Faktorenanalyse nach abgrenzbaren Teilmengen von Variablen sucht. Innerhalb jeder Teilmenge sind die betreffenden Variablen hoch miteinander korreliert, was auf eine gemeinsame Dimension hinweist (z. B. deuten hohe Korrelationen von Variablen wie Häufigkeit des Theaterbesuches, Interesse an Kultursendungen und klassischer Musik auf eine hochkulturelle Dimension hin). Abgrenzbar werden die Teilmengen dadurch, dass die ihnen zugehörigen Variablen zwar miteinander (intern) hoch korrelieren, aber mit den Variablen aller anderen Teilmengen nicht oder kaum zusammenhängen (so gibt es weitere kulturelle Dimensionen von Freizeittätigkeiten, etwa die Dimension der Trivialität). Der dimensionalen Beschreibung einer Reihe von Variablen dient eine weitere multivariate Verfahrensklasse, die als Skalierungsverfahren bezeichnet wird. Im Unterschied zur Faktorenanalyse sind sie i. d. R. nur auf eine einzige Dimension ausgerichtet. Ein wichtiges Verfahren ist die Reliabilitätsanalyse, die die interne Konsistenz eines Variablensatzes (entspricht einer Teilmenge in der Faktorenanalyse) beschreibt. Je höher die Variablen miteinander korrelieren, desto höher ist auch ihre interne Konsistenz und desto eher lassen sie sich als Indikatoren einer gemeinsamen Dimension interpretieren. Skalierungsverfahren und Faktorenanalyse dienen einer gemeinsamen Erkenntnisabsicht mit überaus großer Bedeutung für die Psychologie und Sozialwissenschaften: der Identifikation von Dispositionsvariablen (Intelligenz, Persönlichkeitstendenzen, Einstellungen, Verhaltensneigungen u. a.). Diese bes. Art von Variablen kann sowohl als abhängige als auch als ursächliche Größe in die statistische Kausalanalyse (s. Regressionsanalyse) eingehen.

4.3 Gruppenbildende Verfahren

Von gänzlich anderer Art sind Klassifikationsverfahren (clusteranalytische Verfahren), deren primäres Ziel darin besteht, Untersuchungsobjekte (Individuen, Städte, Texte, geografische Räume etc.) in Klassen bzw. Gruppen einzuteilen. Bei aller Unterschiedlichkeit einer Vielzahl von Verfahren und Vorgehensweisen (für verschiedene Skalierungsniveaus) lässt sich ein gemeinsamer Grundgedanke von Klassifikationsverfahren ausmachen: Objekte, die einer Klasse zugeordnet werden, sollen möglichst gleichartig (homogen), die Klassen untereinander aber möglichst unterschiedlich (heterogen) sein. Die Ähnlichkeit bzw. Unähnlichkeit von Objekten wird mit einer großen Auswahl entspr.er Maßzahlen ermittelt. In der praktischen Anwendung können bspw. soziale Milieus (etwa die SINUS-Milieus) identifiziert werden, indem Personen anhand einer Vielzahl sozialstrukturell relevanter Variablen (Einkommen, Bildung, Alter, Lebensziele, kulturelle Stile) einer Clusteranalyse unterzogen werden. Jedes statistisch auffindbare Milieu zeichnet sich durch eine spezifische Merkmalskombination aus (so ist das Milieu der „Hedonisten“ eine Gruppe mit niedriger Bildung, jungem Alter und hoher Erlebnisorientierung).

5. Analyse zeitbezogener Daten

Für die Analyse von Veränderungen im Zeitablauf bietet die S. verschiedene Ansätze und Instrumentarien. Zeitreihen entstehen, wenn ein Merkmal, z. B. der Preis eines Gutes, in bestimmten – meist gleichen – Zeitabständen (z. B. Tage, Monate, Jahre) gemessen wird. Ist man nicht nur an einem einzelnen Objekt, sondern an der zeitlichen Entwicklung einer Gesamtheit von Objekten interessiert, bildet man zusammenfassende Indizes. Der Verbraucherpreisindex z. B. misst die durchschnittliche Preisentwicklung von Waren und Dienstleistungen in Haushalten und dient der Ermittlung der Inflationsrate. Ein anderer Index ist der DAX, ein gewichteter Börsenindex, der sich aus den 30 wichtigsten Aktientiteln zusammensetzt. Die Zeitreihenanalyse ist bestrebt, die gemessenen Größen mit Hilfe regressionsanalytischer Verfahren in spezifische, zeitbezogene Komponenten zu zerlegen. Zu unterscheiden sind der generelle, langfristige Trend einer Entwicklung (schließt auch Stabilität ein), zyklische Verläufe sowie saisonal wiederkehrende Schwankungen.

Bei der Verfahrensgruppe, die unter dem Begriff Lebensdauer- und Ereignisanalyse zusammengefasst wird, geht es – anders als bei der Zeitreihenanalyse – um die Analyse von Zeitintervallen zwischen zwei definierten Ereignissen bzw. Zuständen. Beispiele hierfür sind die Überlebenszeiten von Patienten in medizinischen Studien, die Dauer der Arbeitslosigkeit, die Ehedauer bis zur Scheidung, die Dauer von UN-Einsätzen oder die Dauer bis zum Wechsel der Parteipräferenz. Ziel der Analyse ist es, die betreffenden Zeit- bzw. Überlebensdauern zu beschreiben und Ereignisse bzw. Zustandsänderungen zu erklären. So kann man z. B. versuchen, die Dauer von UN-Einsätzen in Abhängigkeit vom Konflikttyp zu erklären.

In letzter Zeit gewinnt in den Sozialwissenschaften die statistische Analyse von Paneldaten an Bedeutung. Bei diesem Datentypus liegen für einzelne Merkmalsträger Informationen (z. B. über das Einkommen) vor, die über mehrere Messzeitpunkte hinweg erhoben wurden. Durch den Vorher-Nachher-Vergleich dieser Informationen gelingt eine Annäherung an die experimentelle Analyselogik, was die kausale Analyse von Massendaten erheblich verbessert. In diesem Zusammenhang wurden mit Fixed Effects-Modellen spezielle Varianten der Regressionsanalyse entwickelt, die eine ansonsten nicht durchführbare Kontrolle unbeobachteter Drittvariablen erlaubt.

6. Inferenzstatistik

Allg. gesprochen will die Inferenz-S. (induktive S.) darüber informieren, inwieweit man sich auf eine Stichprobe verlassen und aus ihr Rückschlüsse auf die eigentlich interessierende Grundgesamtheit ziehen kann. Man spricht von Repräsentations- bzw. Induktionsschluss. Wird z. B. bei 2 000 Personen das durchschnittliche Nettoeinkommen ermittelt, so kann man dieses für die gesamte (Mio. Personen zählende) Erwerbsbevölkerung mit geringem Irrtumsrisiko auf etwa 100 Euro genau abschätzen. Neben dieser Schätzproblematik geht es in der induktiven S. v. a. um Signifikanztests. Für die Präzision und Gültigkeit eines Induktionsschlusses ist nicht die Größe der Grundgesamtheit ausschlaggebend, sondern lediglich die Größe der Stichprobe sowie deren Qualität (es muss sich um eine Zufallsstichprobe handeln). Das theoretische Instrumentarium der induktiven S. kommt aus der Wahrscheinlichkeits- sowie aus der Schätz- und Testtheorie.

Ein grundlegendes Theorem der Inferenz-S. ist der zentrale Grenzwertsatz, der in seiner allg.sten Form besagt, dass die Ergebnisse von Zufallsprozessen annähernd so verteilt sind wie eine Normalverteilung (Gauß’sche Glockenkurve), wenn viele Zufallseffekte zusammenwirken. In der praktischen Anwendung geht man z. B. davon aus, dass Stichprobenmittelwerte ab einem Stichprobenumfang von 30 Fällen normalverteilt sind. Gedankenexperimentell kann man sich dies so vorstellen, dass unendlich viele Stichproben eines bestimmten Umfangs (jeweils 30 oder mehr Fälle) gezogen und alle sich ergebenden Mittelwerte in einer Häufigkeitsverteilung – die dann in etwa der Normalverteilung entspricht – dargestellt werden. Ähnliche Überlegungen lassen sich für die Verteilung von Stichprobenanteilen (Prozentsätze) und anderen Kennwerten anstellen. Auf der Grundlage der (standardisierten) Normalverteilung kann man im Umkehrschluss angeben, wie wahrscheinlich das Ergebnis einer konkreten Stichprobe ist, wenn man bestimmte Annahmen über die Grundgesamtheit trifft. Dieses wahrscheinlichkeitstheoretische Fundament macht man sich beim Schätzen und Testen in unterschiedlicher Weise zunutze.

Beim Schätzen wird eine untere und eine obere Grenze (Vertrauens- oder Konfidenzintervall) berechnet, innerhalb derer mit einer gewissen Sicherheit (Konfidenzniveau) der zu schätzende Wert (z. B. besagtes durchschnittliches Nettoeinkommen) in der Grundgesamtheit liegt. So bedeutet ein Konfidenzniveau von 95 %, dass die berechneten Grenzen in 95 % aller denkbaren Stichproben den wahren Wert der Grundgesamtheit enthalten. Daneben werden Punktschätzungen vorgenommen, die exakte Schätzwerte angeben, ohne allerdings deren Unsicherheitsbereiche zu quantifizieren. Im einfachsten Fall wird der betreffende Kennwert der Stichprobe entnommen (z. B. das durchschnittliche Nettoeinkommen). Dies setzt jedoch voraus, dass der betreffende Schätzer erwartungstreu ist. Damit ist gemeint, dass ein zu schätzender Wert im Durchschnitt aller denkbaren Stichproben mit dem tatsächlichen Wert der Grundgesamtheit übereinstimmt. Auf den Mittelwert und Prozentsätze trifft dies z. B. zu, nicht jedoch auf die Stichprobenvarianz, die zur Schätzung der Varianz in der Grundgesamtheit entspr. korrigiert werden muss.

Beim statistischen Hypothesentest, der in der Forschungspraxis einen überaus hohen (z. T. sogar übersteigerten) Stellenwert einnimmt, wird die Signifikanz eines Stichprobenergebnisses überprüft. Im Grunde geht es darum, Stichprobenergebnisse gegen unvermeidliche Zufallsschwankungen abzusichern. Hypothesentests basieren auf zwei konkurrierenden Hypothesen, der Null- und der Alternativhypothese. Die zu überprüfende Nullhypothese beschreibt die Annahme, dass ein Stichprobenergebnis (z. B. ein gefundener Einkommensunterschied zwischen zwei Bevölkerungsgruppen) lediglich zufallsbedingt ist. Die Alternativhypothese (relevante Forschungshypothese) hingegen besagt, dass ein bestimmtes Ergebnis eben nicht mehr durch den Zufall zu erklären ist, sondern tatsächlich etwas über die Verhältnisse in der Grundgesamtheit aussagt (z. B. über die Existenz eines Einkommensunterschiedes). Die S. bietet eine Vielzahl von Tests für unterschiedliche Kennwerte bzw. Fragestellungen. So können neben Mittelwert- und Anteilsunterschieden z. B. auch statistische Zusammenhänge (Korrelationen) oder bestimmte Parameter (Regressionskoeffizienten u. a.) auf Signifikanz geprüft werden. Um über die Annahme oder Ablehnung der Nullhypothese zu entscheiden, wird eine Prüfgröße berechnet, die einer bestimmten Wahrscheinlichkeitsverteilung (häufig der Normalverteilung) folgt. Überschreitet diese Größe einen festgelegten Wert, den kritischen Wert, so wird die Nullhypothese verworfen und die Alternativhypothese als bestätigt betrachtet. Der kritische Wert ergibt sich aus dem gewünschten Signifikanzniveau α; es beschreibt die Wahrscheinlichkeit – auch als α-Fehler bezeichnet – eine korrekte Nullhypothese fälschlicherweise zu verwerfen. Üblicherweise wird der α-Fehler auf 0,05 (5 %) festgelegt. Unter der Bedingung, dass die Nullhypothese in der Grundgesamtheit richtig ist, würde man in diesem Fall dennoch bei 5 % aller möglichen Stichproben rein zufallsbedingt ein Ergebnis erhalten, das irrtümlich dazu führt, die Nullhypothese zu verwerfen. Die zweite Art von Entscheidungsfehler ist der ß-Fehler, den man dann begeht, wenn man eine Nullhypothese akzeptiert, obwohl die Alternativhypothese zutrifft.

Vermehrt werden in der Inferenz-S. innovative bzw. weniger voraussetzungsreiche Verfahren eingesetzt. Eines ist das Bootstrapping, eine Computersimulationstechnik, mit der die theoretisch unbekannte Verteilung eines Stichprobenkennwertes auf der Grundlage wiederholter Zufallsauswahlen aus einer gegebenen Stichprobe (die für die Grundgesamtheit steht) ermittelt wird. Das Verfahren ist mittlerweile Bestandteil vieler Softwarelösungen. Als eine Alternative zur klassischen Vorgehensweise der Inferenz-S. gewinnt die Bayes-S. an Bedeutung. Für induktive Rückschlüsse verwendet sie einen anderen, wissensbasierten Wahrscheinlichkeitsbegriff und nutzt zusätzlich Informationen, die über das betreffende Problem bekannt sind.

7. Grenzen, Probleme und Herausforderungen

Abschließend ist auf ausgewählte Grenzen, Probleme und Herausforderungen der S. hinzuweisen. Zudem sind Entwicklungen zu beobachten, die einer kritischen Reflexion bedürfen.

7.1 Objektivität und Subjektivität

Trotz aller immer wieder an der statistischen Denkweise geübten Kritik (z. B. „Lügen mit S.“) ist sie eines der wichtigsten Instrumentarien wissenschaftlicher Objektivität. Die Beschreibung und Analyse der Wirklichkeit mit zahlenmäßigen Massendaten bietet Erkenntnispotenziale, deren Reichweite und Objektivitätsgrad alternativen Formen der Wirklichkeitsbetrachtung (z. B. qualitative Sozialforschung) weitaus überlegen sind, sofern es um große Kollektive geht. Dennoch ist S. immer auch mit Subjektivität verbunden. Bereits im Verlauf der Datenanalyse sind zwingend Entscheidungen zu treffen, die subjektive Einflüsse unvermeidlich werden lassen (z. B. Auswahl von bestimmten Kennwerten bzw. Modellvarianten). Selbst die Ermittlung statistischer Ergebnisse kann subjektiven Einflüssen unterliegen, ohne dass von Manipulation oder gar Fälschung zu sprechen wäre (so ist die in einer Faktorenanalyse zu ermittelnde Faktorenzahl nicht rein objektiv festgelegt, sondern muss auch durch Entscheidung bestimmt werden). Schließlich sind statistische Ergebnisse für sich genommen i. d. R. noch nicht substanzwissenschaftlich bedeutsam, das werden sie erst durch inhaltliche Interpretation (die ebenfalls nicht frei von Subjektivität ist). Entscheidend aber ist, dass subjektive Einflüsse begründbar und damit in der wissenschaftlichen Gemeinschaft kritisiert oder auch anerkannt werden können.

7.2 Signifikanz und Relevanz

Äußerst kritisch ist zu bewerten, wenn statistische Signifikanz als Höhe- und Schlusspunkt der Datenanalyse betrachtet wird. Erstens basieren viele Datenerhebungen, insb. in den Sozialwissenschaften, nicht auf Zufallsstichproben, wodurch die gesamte induktive S. streng genommen nicht mehr anwendbar ist (dennoch sind auch dann Aussagen zur Signifikanz sinnvoll, wenn man sie unter den Vorbehalt stellt, dass sie gültig wären, wenn man eine Zufallsstichprobe hätte). Zweitens findet man schon aus reinem Zufall irgendwann ein signifikantes Ergebnis, wenn eine bestimmte Hypothese nur häufig genug getestet wird. Beim sog.en multiplen Testen wächst der α-Fehler systematisch an. Drittens – und dies ist am wichtigsten – muss streng zwischen der Signifikanz und der Relevanz von Ergebnissen unterschieden werden. Die Aussage, ein Stichprobenbefund (etwa der Einkommensunterschied zweier sozialer Gruppen) sei signifikant, besagt lediglich, dass er aller Wahrscheinlichkeit nach kein Zufallsergebnis ist. Wie problematisch es ist, sich bei statistischen Ergebnissen wesentlich auf deren Signifikanz zu stützen, zeigt sich schon darin, dass mit wachsendem Stichprobenumfang jeder noch so unbedeutende Befund (z. B. ein verschwindend geringer Einkommensunterschied oder Zusammenhang) irgendwann signifikant wird. Signifikanz sagt nichts über die substanzwissenschaftlich viel bedeutsamere statistische Relevanz eines Ergebnisses aus. Diese lässt sich mit geeigneten Maßen der Effektstärke (z. B. erklärte Varianz, Cohens d etc.) erfassen. Es ist also immer danach zu fragen, ob ein signifikantes Ergebnis auch wirklich relevant ist.

7.3 Verfahrensfetischismus

Die Entwicklung und Anwendung statistischer Verfahren hat in den letzten Jahrzehnten, auch dank immer größerer elektronischer Rechenkapazitäten, rasant zugenommen. Insb. in der multivariaten Datenanalyse ist eine zunehmende Komplexitätssteigerung und Diversifizierung statistischer Analysemethoden zu beobachten. Diese Entwicklung ist einerseits zu begrüßen, da so neue und verbesserte (wenn auch häufig sehr spezielle) Analysemöglichkeiten zur Verfügung gestellt werden. Andererseits besteht die Gefahr eines Verfahrensfetischismus, wenn die Gültigkeit statistischer Ergebnisse ausschließlich vom verwendeten Verfahren abhängig gemacht wird. Oft unterscheiden sich scheinbar unterschiedliche Verfahren im forschungspraktischen Gebrauch jedoch nur geringfügig hinsichtlich ihrer inhaltlichen Ergebnisse. Zudem können empirische Forschungsfragen vielfach auch durch weniger komplexe und fehleranfällige sowie leichter nachvollziehbare statistische Modelle beantwortet werden.

7.4 Statistische Grundbildung

Eine der wichtigsten bildungspolitischen Herausforderungen besteht darin, möglichst weiten Teilen der Bevölkerung eine statistische Grundbildung zukommen zu lassen. Nur wer ein Grundverständnis wichtiger statistischer Konzepte hat, kann heute noch gesellschaftlich bedeutsame Entwicklungen und Probleme (z. B. Klimaerwärmung), die mehr und mehr der statistischen Analyse bedürfen, angemessen nachvollziehen. Gesellschaftliche Aufklärung ist in einer ungewissen Welt ohne S. nicht mehr möglich. Auch kompetente persönliche und professionelle Entscheidungen (z. B. hinsichtlich der Vermeidung gesundheitlicher Risiken) sind zunehmend auf die Nutzung statistischen Wissens angewiesen.

Autoren

Thomas Müller-Schneider, Matthias Voigt

Literatur

S. E. Ahmed: Big and Complex Data Analysis, 2017 • T. Schröder: Treasure Hunt in the Data Jungle, 2017 • K. Backhaus u. a.: Multivariate Analysemethoden, 2016 • L. Fahrmeier u. a.: Statistik, 2016 • J. Behnke: Logistische Regressionsanalyse, 2015 • H. Best u. a.: Regression Analysis and Causal Inference, 2015 • K. Schüller: Statistik und Intuition, 2015 • P. P. Eckstein: Repetitorium Statistik, 2014 • S. L. Morgan: Handbook of Causal Analysis for Social Research, 2014 • M. Giesselmann u. a.: Regressionsmodelle zur Analyse von Paneldaten, 2012 • D. Urban u. a.: Regressionsanalyse, 2011 • J. Bortz u. a.: Statistik für Human- und Sozialwissenschaftler, 2010 • D. Boyd: Privacy and Publicity in the Context of Big Data, 2010 • M. Eid u. a.: Statistik und Forschungsmethoden, 2010 • H. Kromrey: Empirische Sozialforschung, 2009 • R. Schnell u. a.: Methoden der empirischen Sozialforschung, 2008 • H. Benninghaus: Deskriptive Statistik, 2007 • A. Diekmann: Empirische Sozialforschung, 2007 • S.-M. Kühnel u. a.: Statistik für die Sozialwissenschaften, 2006 • A. Quantemberg: Das Signifikanz-Relevanz-Problem beim statistischen Testen von Hypothesen, 2005.

Empfohlene Zitierweise

Zitation kopieren

T. Müller-Schneider, M. Voigt: Statistik, Version 08.06.2022, 09:10 Uhr, in: Staatslexikon⁸ online, URL: https://www.staatslexikon-online.de/Lexikon/Statistik (abgerufen: 27.11.2024)

Lizenz

https://creativecommons.org/licenses/by-nc-nd/4.0/deed.de