Ökonometrie
Einordnung, Anwendung und Forschungsgebiete
Gelang es der Bundesregierung mit den im Jahr 2005 wirksam gewordenen Hartz-IV-Gesetzen die ausufernde Arbeitslosigkeit und die damit einhergehende Belastung der Sozialkassen erfolgreich zu bekämpfen? Je nach politischer Grundüberzeugung und persönlichen Erfahrungen werden die Antworten auf diese Frage sehr unterschiedlich ausfallen. Um zu einer objektiveren Antwort zu gelangen, versuchen Ökonomen relevante Daten zu sammeln, welche den tatsächlichen wirtschaftlichen Zustand vor und nach der Einführung der Hartz-IV-Gesetze beschreiben. Beispiele für solche Daten sind die Arbeitslosenzahlen, die Wachstumsraten des BIP sowie die Anzahl der Bevölkerung im erwerbsfähigen Alter. Die Ökonomen werten diese Daten mit Hilfe von statistischen Methoden aus. Darunter sind zahlreiche Standardmethoden der Statistik, die auch in anderen Wissenschaftsfeldern regelmäßig genutzt werden, aber auch einige statistische Methoden, die speziell für wirtschaftswissenschaftliche Fragestellungen entwickelt wurden. Dieses Bündel aus allgemeinen und spezifisch wirtschaftswissenschaftlichen Statistikmethoden wird als Ö. bezeichnet.
Ökonometrische Analysen sind oftmals komplex und erfordern gezielt ausgebildete Ökonomen. Sie sind in der Lage, numerische Abschätzungen der Wirkungszusammenhänge zu berechnen. Es ist kein Zufall, dass in den Universitäten die Ö. inzwischen zum Standardkanon der wirtschaftswissenschaftlichen Ausbildung zählt.
1. Wissenschaftliche Einordnung
In der Wissenschaft wird ganz allgemein zwischen theoretischer und empirischer Forschung unterschieden. Die theoretische Forschung leitet aus grundlegenden Annahmen gehaltvolle Thesen ab, mit denen die Realität erklärt werden soll. Die empirische Forschung konfrontiert diese Theorien mit der Realität, also mit den empirischen Beobachtungen.
Beide Arbeitsbereiche sind wichtig, um die Realität zu verstehen. Das gilt in ganz besonderem Maße für die Wirtschaftswissenschaft. Dort ist Theorie ohne Empirie von geringer Relevanz für die Praxis. Umgekehrt ist auch die Empirie ohne eine Theorie wenig gehaltvoll. Studien, welche Theorie und Empirie verknüpfen, finden in der wirtschaftswissenschaftlichen Forschung die größte Beachtung. Auch der Transfer in die Praxis gelingt bei solchen Studien deutlich leichter.
Je nachdem wie die beobachteten Fakten zustande kommen, unterscheidet man bei der empirischen Wirtschaftsforschung zwischen der historischen und der experimentellen Variante. Beide Varianten greifen auf ökonometrische Auswertungsmethoden zurück.
In der historischen Variante der Empirie wird ein theoretisches Modell mit Fakten der Vergangenheit konfrontiert. Als empirische Fakten werden Zustände und Entwicklungen herangezogen, die sich im Laufe der Geschichte ergeben haben. Die Geschichte kann dabei sehr kurzfristig sein. Der Ölpreis des Vortags ist genauso empirischer Fakt wie die Erfindung der Dampfmaschine.
Anders sieht es bei der experimentellen Variante der empirischen Forschung aus. Dort entstammen die Fakten einem kontrollierten Experiment. Ersonnen wurde das Experiment, um eine Theorie ganz gezielt mit empirischen Fakten zu konfrontieren. Das Versuchslabor ist der Prototyp experimenteller Forschung. Ein solches Labor erzeugt einen von der Außenwelt abgeschnittenen Raum. Es blendet den Ablauf und damit auch den Einfluss der Geschichte weitgehend aus.
Die Theorie mit den Fakten zu konfrontieren, erweist sich in der praktischen Umsetzung oftmals als schwierig. Zum einen sind die gesammelten historischen oder experimentellen Fakten nicht immer ausreichend, zum anderen ergeben sich methodische Probleme bei der Auswertung der Fakten. Die typischen Probleme unterscheiden sich dabei von Wissenschaft zu Wissenschaft. Im Vergleich zu anderen Sozialwissenschaften werden in der Wirtschaftswissenschaft die Theorien stärker mathematisch formalisiert. Ferner werden die Fakten, auf die eine Theorie angewandt wird, als Daten systematisiert. Daten sind Fakten oder Tatsachen, die in messbarer Form vorliegen. In der Wirtschaftswissenschaft werden demnach formalisierte Theorie und messbare Daten verknüpft. Die Verknüpfung erfolgt mit den Methoden der Statistik.
Mit der Statistik werden die in den Daten enthaltenen Informationen verdichtet. So werden Einsichten gewonnen, die für oder gegen die Gültigkeit einer wirtschaftswissenschaftlichen Theorie sprechen. Die Anwendung statistischer Methoden in diesem Sinne wird als Ö. bezeichnet. Eine wirklich präzise Definition des Begriffes „Ö.“ ist jedoch kaum möglich. Ludwig von Auer beschreibt den Begriff folgendermaßen: „Die Ökonometrie analysiert anhand von beobachtbaren Daten (ökonomische Realität) ökonomische Wirkungszusammenhänge (ökonomische Theorie). Dabei greift sie auf Methoden zurück, die in der statistischen Theorie entwickelt wurden“ (Auer 2016: 3).
Das Wort „Ö.“ (oder in Englisch: econometrics) wird zumeist auf den von Ragnar Frisch verwendeten französischen Begriff économétrie zurückgeführt. R. Frisch ist einer der wichtigen Wegbereiter für diesen Wissenschaftszweig. Er erzählt, dass er darauf hingewiesen wurde, dass Pawel Ciompa bereits im Jahr 1910 ein deutschsprachiges Buch veröffentlichte, in dessen Titel der Begriff „Oekonometrie“ auftauchte. Ein Blick auf die Publikation von P. Ciompa zeigt allerdings, dass er unter diesem Begriff nicht das verstand, was R. Frisch darunter verstand und was auch heute noch darunter verstanden wird.
2. Empirisches Anwendungsbeispiel
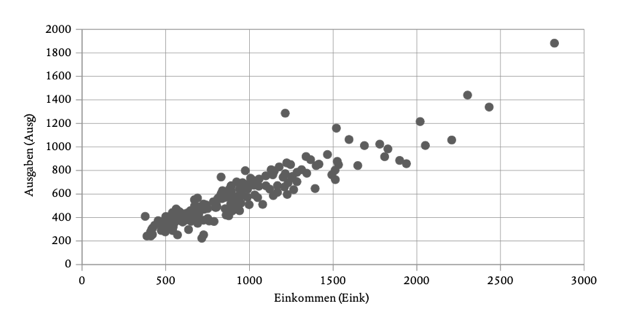
Innerhalb der Ö. existieren mittlerweile viele verschiedene Anwendungsrichtungen und Forschungsgebiete. Trotz dieser Vielfalt gibt es einige Gemeinsamkeiten. Mit etwas Mut zur Vereinfachung lassen sich vier aufeinander aufbauende Schritte ökonometrischer Analyse unterscheiden. Um diese zu veranschaulichen, werden hier die von Edouard Decpetiaux erhobenen belgischen Haushaltsdaten betrachtet, die auch Ernst Engel zur Verfügung standen, als er den Zusammenhang zwischen dem Haushaltseinkommen (Einkommen; Haushalt, privater) und den Ausgaben für Nahrung untersuchte. Er kam damals zu dem Schluss, dass der Anteil der Nahrungsausgaben an den Gesamtausgaben sinkt, wenn das Haushaltseinkommen steigt (Engel’sches Gesetz).
Jeder Punkt in Abb. 1 repräsentiert einen der 198 erfassten belgischen Haushalte. Auf der horizontalen Achse ist das Einkommen dieses Haushalts abzulesen und auf der vertikalen Achse seine Nahrungsausgaben.
Der erste Arbeitsschritt ökonometrischer Analyse ist die sogenannte Spezifikation des ökonometrischen Modells. In diesem Schritt wird der Zusammenhang zwischen dem Einkommen (Variable Eink) und den Nahrungsausgaben (Variable Ausg) in die Form einer mathematischen Gleichung gegossen. Die Punktwolke in Abb. 1 vermittelt den Eindruck, dass der „wahre Zusammenhang“ zwischen den Variablen Eink und Ausg linear ist, also durch eine Gerade beschrieben werden kann. Diese Gerade lässt sich mathematisch in der folgenden Form schreiben:
Ausg = α + β • Eink
Dabei werden α und β als Parameter bezeichnet. Sie legen den genauen Verlauf der Gerade fest. In der Grafik ist der Parameter α der Schnittpunkt der Geraden mit der vertikalen Achse. Der Parameter β ist die Steigung der Gerade. Er gibt an, um wie viele Einheiten man sich auf der Geraden nach oben bewegt, wenn man eine Einheit nach rechts wandert. Der Wert des Parameters β sagt also, um wie viel belgische Franken die Nahrungsausgaben normalerweise zunehmen, wenn im Haushalt ein zusätzlicher Franken Einkommen zur Verfügung steht.
Abb. 1: Der Zusammenhang zwischen dem Haushaltseinkommen (Eink) und den Nahrungsausgaben (Ausg); Datenquelle: Decpetiaux (1855).
Grafisch gesprochen geht man demnach davon aus, dass der wahre Zusammenhang durch eine Gerade beschrieben werden kann, die in etwa „mittig“ durch die abgebildete Punktwolke verläuft, also möglichst gut in die Punktwolke passt. Aus den Daten der Punktwolke die am besten passende Gerade zu finden, ist der zweite Arbeitsschritt der ökonometrischen Analyse. Dieser Schritt wird als die Schätzung des Modells bezeichnet. Das Auffinden der am besten passenden Gerade ist ein Festlegen auf bestimmte Parameterwerte α und β.
Das populärste Schätzverfahren ist die Methode der kleinsten Quadrate. Computer rechnen in Sekundenbruchteilen das jeweilige Ergebnis aus. Für den in der Abb. 1 dargestellten Datensatz ergibt sich die eingezeichnete Gerade. Sie besitzt die Parameterwerte α = 84,10 und β = 0,53. Demnach errechnen sich die Nahrungsausgaben aus einem Sockelbetrag von 84,10 Franken zzgl. weiterer 0,53 Franken pro Franken Einkommen. Bspw. würde ein Haushalt mit 1 000 Franken Einkommen schätzungsweise 84,10 + 0,53 • 1 000 = 614,10 Franken für Nahrung aufwenden.
Die Methode der kleinsten Quadrate ist für die Schätzung nicht immer die beste Wahl. Deshalb stehen in der Ö. inzwischen unzählige weitere Schätzverfahren zur Verfügung, die je nach Datenlage und Untersuchungsgegenstand zum Einsatz kommen.
Es ist üblich, im Anschluss an die Schätzung einen dritten Arbeitsschritt ökonometrischer Analyse auszuführen. In diesem dritten Schritt wird eine Behauptung aufgestellt, die es empirisch zu überprüfen gilt. Dies wird als Hypothesentest bezeichnet. Das Engel’sche Gesetz behauptet, dass der Anteil des Einkommens, der für Nahrungsausgaben aufgewendet wird, bei steigendem Einkommen fällt. Stützen die bisherigen Ergebnisse diese Behauptung?
Obige Gleichung kann auf beiden Seiten des Gleichheitszeichens durch die Variable Eink dividiert werden. Es ergibt sich:
Ausg/Eink = α/Eink + β
Der Bruch (Ausg/Eink) auf der linken Seite des Gleichheitszeichens ist der Anteil der Nahrungsausgaben am Einkommen. Dieser Anteil ergibt sich demnach aus der Summe von β und dem Wert des Bruches (α/Eink).
Die Methode der kleinsten Quadrate lieferte die Schätzwerte α = 84,10 und β = 0,53. Gemäß dieser Schätzung liegt bei einem Einkommen von 1 000 Franken der Anteil, der in Nahrungskäufe geht, bei 84,10/1 000 + 0,53 = 61,4 %, während er bei einem Einkommen von 2 000 Franken lediglich 84,10/2 000 + 0,53 = 57,2 % beträgt. Demnach fällt bei steigendem Einkommen der Anteil der Nahrungsausgaben am Einkommen. Dies war genau die Behauptung E. Engels. Das empirische Ergebnis aus der Methode der kleinsten Quadrate stützt also E. Engels These.
Mathematisch erklärt sich das Resultat folgendermaßen: Um den Anteil der Nahrungsausgaben am Einkommen (Ausg/Eink) zu erhalten, wird der Wert des Bruches (α/Eink) zu β hinzuaddiert. Jedoch fällt der Wert von (α/Eink) bei steigendem Einkommen immer kleiner aus. Deshalb sinkt auch der Wert von (Ausg/Eink). Wäre α hingegen negativ, würde in der Berechnung von (Ausg/Eink) der Betrag von (α/Eink) vom Wert β abgezogen werden. Der Abzug fällt jedoch umso geringer aus, je größer Eink. Das bedeutet, dass der Wert von (Ausg/Eink) bei steigendem Einkommen steigt – was einen Widerspruch zur Behauptung E. Engels darstellen würde. Es lässt sich deshalb festhalten: Der aus den Daten ermittelte positive Schätzwert für α passt zum Engel’schen Gesetz, ein negativer Schätzwert für α hätte hingegen dem Gesetz widersprochen.
Nun könnte eingewendet werden, dass der hier ermittelte positive α-Wert eine Zufälligkeit der Stichprobe war. Eine andere Stichprobe belgischer Haushalte hätte eventuell zum umgekehrten Ergebnis geführt. Mit Hilfe ökonometrisch-statistischer Testverfahren lässt sich genauer ermitteln, wie verlässlich das aus der betrachteten Stichprobe gewonnene Ergebnis tatsächlich ist.
Im vierten Arbeitsschritt ökonometrischer Analyse können sogenannte Prognosen vorgenommen werden. Bspw. könnte man „prognostizieren“, wie groß damals die Nahrungsausgaben eines belgischen Haushalts mit einem Einkommen von 1 000 Franken gewesen wären. Unter Ausnutzung der Ergebnisse der Methode der kleinsten Quadrate ergibt sich:
Ausg = 84,10 + 0,53 • 1 000 = 614,10
Die Prognose hätte also Nahrungsausgaben in Höhe von 614,10 Franken ergeben.
3. Wichtige Forschungsgebiete
Aus Platzgründen konnte hier nur ein einfaches Veranschaulichungsbeispiel für ökonometrisches Arbeiten gegeben werden. Wer einen breiteren Einstieg in die Ö. anstrebt, kann bspw. die Arbeiten von L. von Auer konsultieren. Zu den deutschsprachigen Alternativen zählen Peter Hackl und Christian Dreger u. a., die allerdings etwas umfangreichere Vorkenntnisse voraussetzen. Zu den populären englischsprachigen Einführungsbüchern gehören bspw. R. Carter Hill u. a. oder auch James H. Stock und Mark W. Watson. Etwas anspruchsvoller ist Jeffrey Marc Wooldridge und deutlich anspruchsvoller William H. Greene.
Innerhalb der Ö. lassen sich verschiedene Spezialgebiete identifizieren. Einige dieser Gebiete unterscheiden sich durch den Charakter der zugrundeliegenden Daten. Bspw. waren die Daten von E. Engel sogenannte Querschnittsdaten. Sie erfassten zu einem gegebenen Zeitpunkt verschiedene Objekte (hier: belgische Haushalte). Zeitreihendaten erfassen ein einzelnes Objekt zu verschiedenen Zeitpunkten. Das am Anfang dieses Artikels genannte Beispiel basiert auf Zeitreihendaten. Wenn viele Objekte zu vielen unterschiedlichen Zeitpunkten erfasst werden, dann spricht man von Paneldaten. Sie stellen also eine Kombination aus Querschnitts- und Zeitreihendaten dar. Die empirische Auswertung von Paneldaten erfordert andere ökonometrische Instrumente als die Auswertung von Querschnittsdaten. Die Auswertung von Zeitreihendaten erfordert wiederum andere Instrumente.
Bei der Untersuchung von E. Engel wurden die Nahrungsausgaben eines Haushalts durch sein Einkommen erklärt. Es gibt auch Datensätze, bei denen die zu erklärende Variable nicht metrisch messbar ist, sondern nur zwei Werte annehmen kann wie bspw. „ja“ oder „nein“. So könnte sich eine Bank dafür interessieren, welche Faktoren im Umfeld des Kreditnehmers tendenziell die vollständige Rückzahlung des Kredites („ja“) begünstigen und tendenziell zu Kreditausfall („nein“) führen. Zu den relevanten Faktoren gehören bspw. die Einkommenssituation und das Ausbildungsniveau. Die Auswertung solcher Datensätze erfordert spezielle ökonometrische Techniken, so dass sich auch hier wieder ein eigenes Spezialgebiet der Ö. ergibt.
Die Art des Datensatzes ist jedoch nicht die einzige Trennlinie der verschiedenen Gebiete der Ö. Liegt bspw. ein Datensatz mit Querschnittsdaten vor, so kann dieser mit sehr unterschiedlichen Ansätzen ausgewertet werden. In der Auswertung der Daten von E. Engel wurde ein sogenannter parametrischer Ansatz verwendet. Es existieren jedoch auch sogenannte semi-parametrische und nicht-parametrische Ansätze. Eine weitere Variante der ökonometrischen Methodik ist der Bayesianische Ansatz.
Zu allen Spezialgebieten der Ö. existiert eine umfangreiche Literatur. Peter Kennedy gibt dem Leser einen recht intuitiven Zugang zu den Besonderheiten des jeweiligen Spezialgebiets.
Literatur
L. von Auer: Ökonometrie. Das R-Arbeitsbuch, 2017 • Ders.: Ökonometrie. Eine Einführung, 72016 • J. M. Wooldridge: Introductory Econometrics, 72020 • J. H. Stock/M. W. Watson: Introduction to Econometrics, 42019 • C. Dreger/R. Kosfeld/H. F. Eckey: Ökonometrie, 52014 • W. H. Greene: Econometric Analysis, 82018 • P. Hackl: Einführung in die Ökonometrie, 22012 • R. C. Hill/W. E. Griffiths/G. C. Lim: Principles of Econometrics, 52018 • P. Kennedy: A Guide to Econometrics, 62008 • R. Frisch: Note on the Term ‚Econometrics‘, in: EC 4/1 (1936), 95 • R. Frisch: Sur un Problème d’Économique Pure, Nors Matematisk Forenings Skrifter, 1926 • E. Engel: Die vorherrschenden Gewerbszweige in den Gerichtsämtern mit Beziehung auf die Productions- und Consumtionsverhältnisse des Königreichs Sachsen. II. Das Gesetz der Dichtigkeit, in: Zeitschrift des Statistischen Bureaus des Königlich Sächsischen Ministeriums des Inneren 3/6–7 (1857), 153–182 • E. Ducpetiaux: Budgets Economiques de Classes de Ouvrieres en Belgique, 1855.
Empfohlene Zitierweise
L. Auer: Ökonometrie, Version 08.06.2022, 09:10 Uhr, in: Staatslexikon8 online, URL: https://www.staatslexikon-online.de/Lexikon/%C3%96konometrie (abgerufen: 15.03.2025)