Investition
1. Begriff und Arten
I. bezeichnet die Verwendung finanzieller Mittel zur Beschaffung von Sach-, immateriellem und Finanzvermögen. I.en in Sach- und immaterielles Vermögen sind Real-I.en, I.en in Finanzvermögen werden als Finanz-I.en bezeichnet. Sach-I.en betreffen Anlagen, die direkt (z. B. Maschinen) oder indirekt (z. B. Gebäude, Grundstücke) am Leistungsprozess beteiligt sind. I.en in immaterielles Vermögen sind Lizenzen, Patente, Software und Humankapital (Mitarbeiter). I.en in das Finanzvermögen weisen keine direkte güterwirtschaftliche Komponente auf, sondern begleiten den Leistungsprozess, in dem Darlehen vergeben werden, Kunden Zahlungsziele erhalten (Forderungen) und für die Sicherstellung der jederzeitigen Zahlungsfähigkeit Liquidität (Bankguthaben, Kasse) und kurzfristig liquidierbare Vermögensgegenstände (Wertpapiere) gehalten werden. Zu den Finanz-I.en zählt auch der vollständige oder teilweise Kauf von anderen Unternehmen (Beteiligungen).
Je nach Ziel und Zweck der beabsichtigten Analyse kann ein vermögensorientierter, wirkungsorientierter oder zahlungsorientierter I.s-Begriff zugrunde gelegt werden. Der vermögenorientierte I.s-Begriff versteht eine I. als eine zeitlich befristete Festlegung von finanziellen Mitteln im Anlage- und Umlaufvermögen. I.en transformieren daher finanzielle Mittel in Unternehmensvermögen. Im Rahmen des wirkungsorientierten I.s-Begriffs wird der mit einer I. verbundene Nutzen (sowohl quantitativ als auch qualitativ) den mit ihr verbundenen Kosten gegenübergestellt. In der Betriebswirtschaftslehre vorherrschend ist der zahlungsorientierte I.s-Begriff, der eine I. in Form einer Zahlungsreihe abbildet, die mit einer Anschaffungsauszahlung beginnt und der in der Zukunft Rückflüsse (in Form von Einzahlungen) und gegebenenfalls auch weitere Abflüsse (in Form von Auszahlungen) folgen.
2. Investitionsrechnung bei Sicherheit
Zur Beurteilung von I.s-Projekten kommen I.s-Rechenverfahren zum Einsatz. Diese dienen dem Investor als Grundlage für seine Entscheidungen. Sie lassen sich in Abhängigkeit von der Art und Weise, wie zeitliche Unterschiede der Zahlungen berücksichtigt werden, in statische und dynamische Verfahren unterteilen. Über die den Modellen zugrunde gelegten Annahmen kann die Komplexität und Realitätsnähe der Verfahren gesteuert werden. Im einfachsten Fall werden zukünftige Zahlungen als sicher angenommen. Aufwendiger wird die Analyse, wenn Unsicherheit und damit Risiken modelliert und in die Zahlungsströme integriert werden sollen.
2.1 Statische Verfahren
Statische I.s-Rechenverfahren berücksichtigen zeitliche Unterschiede im Auftreten von Ein- und Auszahlungen nicht oder nur teilweise. Die Verfahren betrachten meist nur einen Zeitabschnitt (im Regelfall ein Jahr) der gesamten I.s-Dauer und unterstellen, dass diese Periode repräsentativ für die gesamte I.s-Dauer ist, oder es werden Durchschnittswerte gebildet. Die Planungsgrößen werden i. d. R. aus der Kosten- und Erlösrechnung gewonnen. Zur Verfügung stehen vier Verfahren, die sich im Umfang der benötigten Informationen unterscheiden: die Kostenvergleichsrechnung, die Gewinnvergleichsrechnung, die Rentabilitätsrechnung und die statische Amortisationsrechnung.
Die Kritik an den statischen Verfahren entzündet sich zum einen an der unzulänglichen Abbildung der zeitlichen Struktur der Zahlungen. Der Zeitwert des Geldes (Geld heute ist mehr wert als Geld in der Zukunft) findet keine Berücksichtigung. Weitere Kritik bezieht sich auf die verwendeten Inputgrößen. Die statischen Verfahren beziehen ihre Daten aus periodischen Informationssystemen, entweder aus der Kostenrechnung in Form von I.s-Kosten und -erlösen pro Periode oder aus der Gewinn- und Verlustrechnung in Form von I.-Aufwendungen und -erträgen. Wie der zahlungsstromorientierte I.s-Begriff aber schon zum Ausdruck bringt, sind für eine I.s-Rechnung Ein- und Auszahlungen (englisch Cashflows) relevant. Nur sie sind in der Lage, die konkreten Zeitpunkte, zu denen die Zahlungen anfallen, sachgerecht abzubilden.
2.2 Dynamische Verfahren
Die dynamischen I.s-Rechenverfahren lösen die Kritik an den statischen Verfahren. Zu ihnen zählen die Kapitalwertmethode, die Annuitätenmethode, die interne Zinsfußmethode und die dynamische Amortisationsrechnung.
Die Kapitalwertmethode ist das gängigste Verfahren. Zielgröße ist der Kapitalwert, der sich errechnet, in dem alle zukünftigen Einzahlungsüberschüsse auf den heutigen Zeitpunkt abgezinst und mit der Anschaffungsauszahlung der I. saldiert werden. Werden aus Vereinfachungsgründen die zukünftigen Zahlungen als sicher unterstellt, erfolgt die Diskontierung mithilfe eines risikolosen Zinses, dessen Höhe den Zeitwert des Geldes reflektiert. Er kann als die vom Investor geforderte Mindestverzinsung interpretiert werden. Führt die Rechnung zu einem positiven Kapitalwert sollte das I.s-Vorhaben durchgeführt werden, da die Einzahlungen aus der I. unter Berücksichtigung des Zeitwerts des Geldes die Auszahlungen übersteigen. Die Methode kann sowohl zur Bewertung von Sach-I.en als auch zur Bewertung von I.en in Humankapital eingesetzt werden.
Wie die Kapitalwertmethode benötigt die interne Zinsfußmethode eine Zahlungsreihe aller mit der I. verbundenen Ein- und Auszahlungen. Anstatt aber wie bei der Kapitalwertmethode einen Kalkulationszins vorzugeben und mit dessen Hilfe den Kapitalwert auszurechnen, wird bei der internen Zinsfußmethode der Kapitalwert mit einem Wert von Null vorgegeben und anschließend der damit verbundene interne Zins ausgerechnet. Ein I.s-Projekt ist dann positiv, wenn der interne Zinsfuß größer ist als die vom Investor angestrebte Mindestverzinsung.
Die Annuitätenmethode entspr. konzeptionell weitestgehend der Kapitalwertmethode. Auch bei ihr werden eine Zahlungsreihe und ein Kalkulationszins benötigt. Die Vorteilhaftigkeit einer I. wird allerdings nicht in Form eines Einmalüberschusses ausgewiesen, sondern der Kapitalwert wird als jährlich gleich hohe Zahlung über die Laufzeit der I. verteilt. Die Annuität gibt den Vermögenszuwachs des I.s-Vorhabens pro Periode an. Als I.s-Rechenverfahren ist die Annuitätenmethode eher ungebräuchlich. Sie findet praktisch ihren Einsatz in der Finanzierung in Form des Annuitätenkredites. Dort bringt die Annuität den periodisch gleich hohen Kapitaldienst (Zins und Tilgung) eines Schuldners zum Ausdruck.
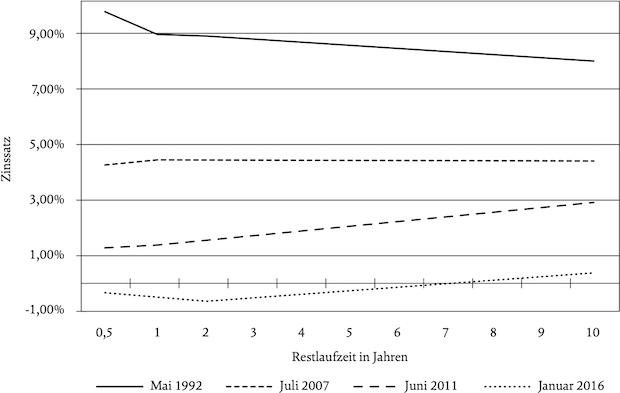
Wird für die Diskontierung der zukünftigen Zahlungen ein für alle Laufzeiten einheitlicher Zins verwendet, entspr. dies implizit der Annahme einer flachen Zinsstrukturkurve. Eine solche konnte empirisch annähernd im Juli 2007 beobachtet werden (vgl. Abb. 1). Dieser Fall ist praktisch aber sehr unrealistisch. Der häufigste Fall ist eine normale Zinsstrukturkurve (Juni 2011), bei der die kürzerfristigen Zinssätze unter den längerfristigen Zinssätzen liegen. Seltener tritt eine inverse Zinsstrukturkurve auf (Mai 1992). In dieser Konstellation liegen die kürzerfristigen Zinssätze über den längerfristigen (vgl. Abb. 1). Seit der Finanzmarktkrise im Jahr 2008 sind an den Kapitalmärkten (Geld- und Kapitalmarkt) auch negative Zinssätze zu beobachten (Januar 2016). Börsennotierte Wertpapiere der BRD mit einer Restlaufzeit von 6 Monaten wiesen erstmals im November 2011 negative Renditen auf. Der Satz der Einlagefazilität der EZB lag im Juni 2014 mit -0,1 % erstmals unter Null.
Die präzise Berücksichtigung der jeweils aktuellen Situation an den Märkten ist insb. in der Finanzbranche von herausragender Bedeutung (z. B. bei der Kalkulation von Bankprodukten). Für die Anwendung der Verfahren in Nicht-Finanzbranchen ist die Annahme der flachen Zinsstrukturkurve hingegen akzeptabel.
3. Investitionsrechnung bei Unsicherheit
Methodisch und konzeptionell sind die vorgestellten dynamischen I.s-Rechenverfahren in der Lage, die unterschiedlichen Zeitpunkte, zu denen Ein- und Auszahlungen anfallen, adäquat zu berücksichtigen. In einer weiteren Ausbaustufe gilt es, auch die Unsicherheit über die Zukunft in den Verfahren abzubilden. Hierzu eignet sich insb. die Szenariotechnik. Mit ihr können die Auswirkungen unterschiedlicher zukünftiger Entwicklungen (z. B. alternative Konjunkturszenarien oder alternative Szenarien für Umsätze, Lohnkosten oder Rohstoffpreise) abgebildet werden. Je größer die Anzahl der alternativen Szenarien ist, desto größer wird die Bandbreite der möglichen I.s-Ergebnisse.
Werden die unsicheren (szenariospezifischen) Rückflüsse zusätzlich mit Eintrittswahrscheinlichkeiten gewichtet und addiert, ergibt sich zu jedem Zeitpunkt ein Erwartungswert der Rückflüsse. Die bisher als sicher unterstellten Cashflows werden durch erwartete Cashflows ersetzt. Typischerweise steigt die Unsicherheit der Zahlungen je weiter diese in der Zukunft liegen. Dies lässt sich rechnerisch durch die Standardabweichung, d. h. die Streuung der Zahlungen um den Erwartungswert zum Ausdruck bringen. Werden in der Kapitalwertformel lediglich die sicheren Cashflows gegen Erwartungswerte der unsicheren Rückflüsse ausgetauscht, würde die Streuung der Zahlungen nicht in die Entscheidung mit einfließen. Um diese ebenfalls zu berücksichtigen, kann die Unsicherheit über eine zusätzliche Risikoprämie in den Kalkulationszins integriert werden (Risikozuschlagsmethode).
Abb. 1: Zinsstrukturkurven im Zeitvergleich; Quelle: Deutsche Bundesbank (2016)
Ein rational handelnder Investor wird ein höheres Risiko in seinem Rechenkalkül berücksichtigen, in dem er eine höhere Verzinsung fordert. Das bekannteste Bewertungsmodell zur Bestimmung der Risikoprämie ist das CAPM, das von William Sharpe, John Lintner und Jan Mossin entwickelt wurde. Die Risikoprämie bringt die angemessene „Entschädigung“ für das Risiko zum Ausdruck, das mit der I. verbunden ist. Somit muss die Risikoprämie umso höher ausfallen, je größer die mit dem I.s-Projekt verbundene Unsicherheit ist.
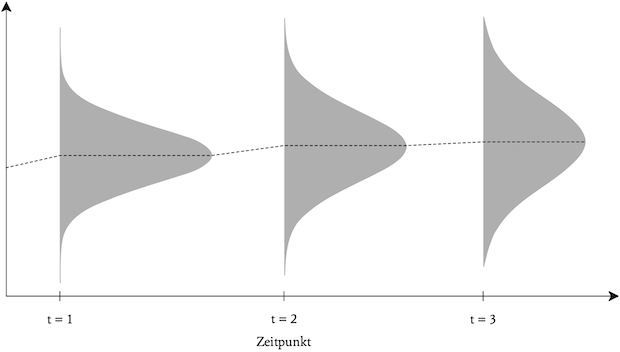
Zu den fortgeschrittenen Verfahren zur Berücksichtigung von Unsicherheit zählen stochastische Szenarioanalysen (auch Bandbreitenverfahren genannt), die auf Simulationen beruhen. In unabhängigen Simulationen wird eine Vielzahl möglicher Zukunftsszenarien für alle definierten Parameter generiert. Jede simulierte Parameterkonstellation stellt ein Szenario dar. Deren Gesamtheit soll eine repräsentative Stichprobe aller möglichen Szenarien widerspiegeln. Zur Veranschaulichung der Ergebnisse einer stochastischen Szenarioanalyse sei in Abb. 2 angenommen, dass die Szenarien einer Normalverteilung unterliegen. Die Normalverteilung unterstellt, dass die Ausprägungen der einzelnen Parameter symmetrisch um den Erwartungswert streuen, wobei der Großteil der Ergebnisse in der Nähe des Erwartungswertes liegt und nur wenige Ausprägungen den Erwartungswert deutlich über- bzw. unterschreiten. Der Grad der Unsicherheit wird über die Stärke der Streuung der Werte um den Erwartungswert zum Ausdruck gebracht.
Ausschlaggebend für die Qualität der Ergebnisse von Bandbreitenverfahren sind die zugrunde gelegten Verteilungsannahmen der einzelnen Parameter. Für die Simulation der Parameter steht eine Vielzahl von Verteilungen zur Verfügungen. Neben der Normalverteilung finden in der Praxis häufig die Dreiecksverteilung und die logarithmische Normalverteilung Anwendung. Bei der Dreiecksverteilung muss neben einem Minimal- und einem Maximalwert für den jeweiligen Parameter auch der wahrscheinlichste Wert angegeben werden. Diese Parameter werden häufig auch im Rahmen der strategischen Planung geschätzt (worst, best and real case).
Abb. 2: Bandbreite von Einzahlungsüberschüssen bei Anwendung der Normalverteilung
Die logarithmische Normalverteilung ist eine rechtsschiefe Verteilung, die nur positive Werte aufweist. Mit ihr kann z. B. der im Zeitverlauf anfallende Aufwand für Reparaturen eines I.s-Projekts simuliert werden. In diesem Fall ist ein natürlicher Nullpunkt gegeben, da Kosten nur anfallen, wenn Reparaturen notwendig sind.
4. Resümee
I.s-Entscheidungen zählen zu den wichtigsten unternehmerischen Entscheidungen. Da mit I.en häufig eine hohe Kapitalbindung und langfristige Bindung einhergeht, sind I.s-Entscheidungen mit besonderer Sorgfalt zu treffen und systematisch in die Risk Governance eines Unternehmens zu integrieren. Der Qualität der Informationen kommt eine herausragende Bedeutung zu. Die Parameter, mit der die zukünftigen Einzahlungsüberschüsse abgebildet werden, sind sorgfältig zu modellieren. Aufgrund der mit I.s-Vorhaben verbundenen Unsicherheit sind Bandbreitenverfahren in besonderem Maße geeignet, die mit I.s-Projekten verbundenen Risiken realistisch abzubilden, um eine fundierte Entscheidung zu ermöglichen. Das I.s-Controlling unterstützt den Entscheider dabei durch Beschaffung, Aufbereitung und Weitergabe der entscheidungsrelevanten Informationen.
Literatur
Deutsche Bundesbank: Zinsstatistik EZB-Zinssätze, 2016 • V. Stein/A. Wiedemann: Risk Governance: Conceptualization, tasks, and research agenda, in: JBE 86/1–2 (2016), 1–24 • H. Schierenbeck/M. Lister/S. Kirmße: Ertragsorientiertes Bankmanagement, Bd. 1, 2014 • Deutsche Bundesbank: Monatsbericht Juli 2013, 2013 • G. Wöhe: Grundzüge der Unternehmensfinanzierung, 2013 • H. Schierenbeck/C. B. Wöhle: Grundzüge der Betriebswirtschaftslehre, 2012 • C. Scholz/V. Stein/R. Bechtel: Human Capital Management, 2011 • B. Nöll/A. Wiedemann: Investitionsrechnung unter Unsicherheit, 2008 • J. Mossin: Equilibrium in a Capital Asset Market, in: EC 34/4 (1966), 768–783 • J. Lintner: The Valuation of Risk Assets and the Selection of Risky Investments in Stock Portfolios and Capital Budgets, in: REST 47/1 (1965), 13–37 • W. F. Sharpe: Capital Asset Prices: A Theory of Market Equilibrium under Conditions of Risk, in: JF 19/3 (1964), 425–442.
Empfohlene Zitierweise
A. Wiedemann: Investition, Version 08.06.2022, 09:10 Uhr, in: Staatslexikon8 online, URL: https://www.staatslexikon-online.de/Lexikon/Investition (abgerufen: 16.04.2025)