Input-Output-Rechnung: Unterschied zwischen den Versionen
K (Input-Output-Rechnung) |
K (Input-Output-Rechnung) |
||
| Zeile 6: | Zeile 6: | ||
<h2 class ="headline-w-margin">2. Konstruktion und Struktur der Input-Output-Tabelle</h2> | <h2 class ="headline-w-margin">2. Konstruktion und Struktur der Input-Output-Tabelle</h2> | ||
<p> | <p> | ||
| − | Das Produktionskonto eines Produktionssektors einer Volkswirtschaft bildet die Grundlage der I. Wie die Abb. des sektoralen Produktionskontos zeigt, enthält dieses auf der linken Seite alle Input-Komponenten und auf der rechten Seite alle Output-Komponenten der [[Produktion]] des | + | Das Produktionskonto eines Produktionssektors einer Volkswirtschaft bildet die Grundlage der I. Wie die Abb. des sektoralen Produktionskontos zeigt, enthält dieses auf der linken Seite alle Input-Komponenten und auf der rechten Seite alle Output-Komponenten der [[Produktion]] des entsprechenden Sektors. Die Input-Seite zeigt die Käufe von Vorleistungen von anderen inländischen Sektoren (z. B. Rohstoffe und Zwischenprodukte einschließlich [[Dienstleistungen]]), die Gütersteuern abzüglich Gütersubventionen, die Arbeitnehmerentgelte im Inland, sonstige Produktionsabgaben abzüglich sonstiger Subventionen, die Abschreibungen, die Importe gleichartiger Güter und den Nettoüberschuss (d. h. der Überschuss nach Abschreibungen). Zur Output-Seite gehören die Verkäufe von Vorleistungen, der Verkauf von Gütern als Konsum- oder Investitionsgüter an inländische Wirtschaftseinheiten und die Exporte. Zu beachten |
</p> | </p> | ||
<p> | <p> | ||
| Zeile 67: | Zeile 67: | ||
<h2 class ="headline-w-margin">3. Analyse der Input-Output-Daten</h2> | <h2 class ="headline-w-margin">3. Analyse der Input-Output-Daten</h2> | ||
<p> | <p> | ||
| − | Die Input-Output-Daten lassen sich für verschiedene strukturelle Analysen verwenden. Um die relative Bedeutung der Vorleistungsströme aufzuzeigen, bietet es sich an, die absoluten Beträge in den jeweiligen Feldern der Input-Output-Tabelle zu normieren. Werden die Beträge in Relation zur Zeilensumme ausgedrückt, ergeben sich | + | Die Input-Output-Daten lassen sich für verschiedene strukturelle Analysen verwenden. Um die relative Bedeutung der Vorleistungsströme aufzuzeigen, bietet es sich an, die absoluten Beträge in den jeweiligen Feldern der Input-Output-Tabelle zu normieren. Werden die Beträge in Relation zur Zeilensumme ausgedrückt, ergeben sich sogenannte Output-Koeffizienten. Sie zeigen, welche Bedeutung einem Sektor für die Erstellung von Vorleistungen und von Gütern für die letzte Verwendung zukommt. Werden die absoluten Beträge der verschiedenen Felder auf die Spaltensummen normiert, ergeben sich die sogenannte Inputkoeffizienten. Sie zeigen, wie bedeutend die Vorleistungen anderer Sektoren sind und wie hoch die Anteile der primären Inputs für die Erstellung der Güter eines Sektors sind. |
</p> | </p> | ||
<p> | <p> | ||
| Zeile 79: | Zeile 79: | ||
</p> | </p> | ||
<p> | <p> | ||
| − | Die direkten und indirekten Wirkungen von Veränderungen der beschriebenen Art lassen sich durch die | + | Die direkten und indirekten Wirkungen von Veränderungen der beschriebenen Art lassen sich durch die sogenannten inversen Koeffizienten angeben. Sie zeigen letztlich wie Multiplikatoren die Gesamteffekte auf und betonen gleichzeitig die möglicherweise sehr unterschiedlichen Wirkungen auf die einzelnen Produktionsbereiche der Volkswirtschaft. Dies sind Informationen, die auch für die [[Wirtschaftspolitik]] relevant sind. Wenn z. B. in einer Rezession gefragt wird, welche Güter der Staat bei Auflage eines Konjunkturprogramms nachfragen soll, um möglichst starke Arbeitsmarkteffekte zu bewirken, kann dies unter Zuhilfenahme der I. beantwortet werden. |
</p> | </p> | ||
<div class="article__information"> | <div class="article__information"> | ||
Aktuelle Version vom 16. Dezember 2022, 06:09 Uhr
1. Die Input-Output-Rechnung als Teil der Volkswirtschaftlichen Gesamtrechnung
Die I. stellt ein Datengerüst dar, das sich mit den Vorleistungsverflechtungen zwischen den verschiedenen Produktionsbereichen innerhalb einer Volkswirtschaft sowie deren Beiträge zum Produktionswert und der Güterverwendung beschäftigt. Sie bildet eine Nebenrechnung der volkswirtschaftlichen Gesamtrechnung, die wiederum als Kern die Berechnung der Inlandsproduktwerte (wie Bruttoinlandsprodukt, Nettoinlandsprodukt, Bruttonationaleinkommen) und der damit zusammenhängenden Strukturaspekte (Entstehungs-, Verwendungs- und Verteilungsrechnung) zum Inhalt hat.
2. Konstruktion und Struktur der Input-Output-Tabelle
Das Produktionskonto eines Produktionssektors einer Volkswirtschaft bildet die Grundlage der I. Wie die Abb. des sektoralen Produktionskontos zeigt, enthält dieses auf der linken Seite alle Input-Komponenten und auf der rechten Seite alle Output-Komponenten der Produktion des entsprechenden Sektors. Die Input-Seite zeigt die Käufe von Vorleistungen von anderen inländischen Sektoren (z. B. Rohstoffe und Zwischenprodukte einschließlich Dienstleistungen), die Gütersteuern abzüglich Gütersubventionen, die Arbeitnehmerentgelte im Inland, sonstige Produktionsabgaben abzüglich sonstiger Subventionen, die Abschreibungen, die Importe gleichartiger Güter und den Nettoüberschuss (d. h. der Überschuss nach Abschreibungen). Zur Output-Seite gehören die Verkäufe von Vorleistungen, der Verkauf von Gütern als Konsum- oder Investitionsgüter an inländische Wirtschaftseinheiten und die Exporte. Zu beachten
| Sektorales Produktionskonto | |
|---|---|
| Käufe (K) von | Verkäufe (V) von |
| Vorleistungen von | Vorleistung an |
| –→ Sektor 1 | –→ Sektor 1 |
| –→ ... | ... |
| –→ Sektor n | –→ Sektor n |
| Gütersteuern und sonstige Produktionsabgaben (T) abzüglich Subventionen (Z) | Konsum der privaten Haushalte und des Staates (C) |
| Arbeitnehmerentgelte (L) | Investitionen (I) |
| Abschreibungen (D) | Exporte (X) |
| Nettoüberschuss (Ü) | |
| Importe gleichartiger Güter (M) | |
Abb. 1: Sektorales Produktionskonto
ist, dass es sich bei den sektoralen Produktionskonten um nicht-konsolidierte Konten handelt, d. h. die Käufe von Vorleistungen von Produktionseinheiten des gleichen Sektors werden nicht gekürzt gegen die – betragsmäßig gleichen – Verkäufe von Vorleistungen an Produktionseinheiten desselben Sektors.
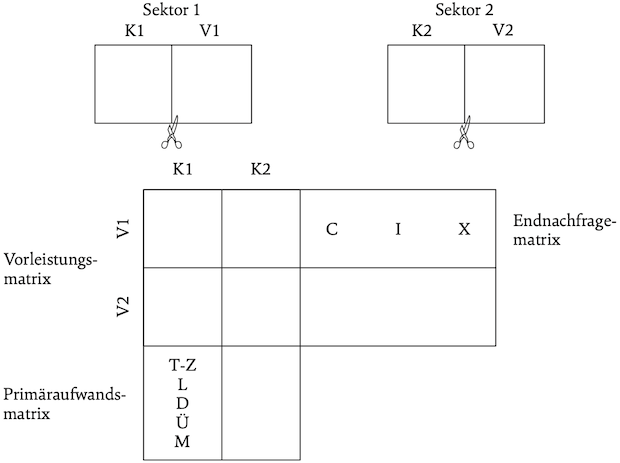
Aus den verschiedenen sektoralen Produktionskonten lässt sich eine Input-Output-Tabelle für die Volkswirtschaft erstellen. Hierbei wird wie folgt vorgegangen: Die linken Seiten jedes sektoralen Produktionskontos werden nebeneinandergelegt und die rechten Seiten um 90 Grad entgegen des Uhrzeigersinnes gedreht und ebenfalls nebeneinandergelegt. Da die Käufe eines Sektors i von einem Sektor j identisch sind mit den Verkäufen des Sektors j an den Sektor i, können die Vorleistungsteile der beiden Seiten übereinandergelegt werden. Die nachfolgende Skizze illustriert dies für den Fall, dass die Volkswirtschaft in nur zwei Sektoren unterteilt wird.
Abb. 2: Die Konstruktion einer Input-Output-Tabelle
Die hierbei entstehende Input-Output-Tabelle hat eine Matrixstruktur. Die Zeilen zeigen die Verwendung der produzierten Güter (Vorleistungen bzw. intermediäre Verwendung und die letzte Verwendung der Güter, d. h. privater und staatlicher Konsum, Investitionen und Exporte). Die Spalten zeigen die Struktur der Input-Komponenten der verschiedenen Sektoren (Vorleistungen bzw. intermediäre Inputs und primäre Inputs). Zeilen- und Spaltensummen sind konstruktionsbedingt gleich. Aus dem Matrixschema der Input-Output-Tabelle lassen sich drei Teile der Matrix unterscheiden: die Vorleistungsmatrix (linker oberer Quadrant), Endnachfragematrix (rechter oberer Quadrant) und Primäraufwandsmatrix (linker unterer Quadrant).
Das StBA gliedert die deutsche Volkswirtschaft in einer stärker untergliederten Version der I. in zwölf Sektoren (z. B. Landwirtschaft, chemische Erzeugnisse, Fahrzeuge, Bauarbeiten, Finanzdienstleistungen und öffentlich Dienstleistungen). In einer tieferen Gliederung umfasst die Darstellung 73 Sektoren.
3. Analyse der Input-Output-Daten
Die Input-Output-Daten lassen sich für verschiedene strukturelle Analysen verwenden. Um die relative Bedeutung der Vorleistungsströme aufzuzeigen, bietet es sich an, die absoluten Beträge in den jeweiligen Feldern der Input-Output-Tabelle zu normieren. Werden die Beträge in Relation zur Zeilensumme ausgedrückt, ergeben sich sogenannte Output-Koeffizienten. Sie zeigen, welche Bedeutung einem Sektor für die Erstellung von Vorleistungen und von Gütern für die letzte Verwendung zukommt. Werden die absoluten Beträge der verschiedenen Felder auf die Spaltensummen normiert, ergeben sich die sogenannte Inputkoeffizienten. Sie zeigen, wie bedeutend die Vorleistungen anderer Sektoren sind und wie hoch die Anteile der primären Inputs für die Erstellung der Güter eines Sektors sind.
Werden die Daten der I. mit wirtschaftstheoretischen Annahmen verbunden, lassen sich Aussagen über die Auswirkungen denkbarer Schocks auf die verschiedenen Bereiche der Volkswirtschaft und die Gesamtwirtschaft untersuchen. Die einfachste Annahme, auf die hierbei zurückgegriffen werden kann, ist die im Zuge der wirtschaftlichen Entwicklung konstante Struktur der Koeffizienten. Man spricht hierbei auch von einer linearen Produktionstechnologie oder auch von der Leontief-Produktionsfunktion.
Anhand einiger Beispiele lässt sich erläutern, welche Fragen sich hierbei untersuchen lassen. Ein Beispiel ist die Untersuchung der Wirkungen einer Lohnerhöhung eines Sektors oder aller Sektoren auf die Preise der Güter der verschiedenen Sektoren. Nimmt man an, dass in einem Sektor i eine bes. preissteigernde Lohnerhöhung erfolgt, wird sich diese in den anderen Sektoren unterschiedlich niederschlagen, da diese die Vorleistungen des Sektors i unterschiedlich intensiv nutzen. Neben den direkten Wirkungen über die Vorleistungen des Sektors i werden die Preise eines anderen Sektors auch dadurch beeinflusst, dass dieser Vorleistungen von verschiedenen Sektoren bezieht, in die wiederum jeweils auch Vorleistungen des Sektors i eingehen. Ähnlich verhält es sich, wenn die Auswirkungen eines Anstiegs von Importpreisen (z. B. bestimmter Rohstoffe) untersucht werden. Sie können z. B. unmittelbar die chemische Industrie betreffen. Da deren Produkte allerdings als Vorleistungen in andere Produkte eingehen, ergeben sich durch die Vielzahl der gekauften Vorleistungen unterschiedliche Wirkungen auf die verschiedenen Sektoren.
Auch die Auswirkungen der Konsum-, Investitions- oder Exportnachfrage auf die verschiedenen Sektoren können mit der I. untersucht werden. Nachfrageänderungen können sich im Prinzip auf alle Sektoren erstrecken oder es kann untersucht werden, welche Folgen eine Veränderung der Nachfrage nach bestimmten Gütern hat. Auch hier berücksichtigt die I., dass direkte und indirekte Wirkungen auftreten. Erhöht sich z. B. die Nachfrage nach Bauleistungen, so führt dies zu einem direkten Effekt in anderen Sektoren aufgrund des Bezugs von Vorleistungen der Hersteller von Bauleistungen aus anderen Sektoren. Da diese anderen Sektoren wiederum Vorleistungen von verschiedenen Sektoren beziehen, beeinflusst dies die Nachfrage nach Gütern anderer Sektoren und es entstehen somit zusätzlich indirekte Effekte auf die Nachfrage in den anderen Sektoren.
Die direkten und indirekten Wirkungen von Veränderungen der beschriebenen Art lassen sich durch die sogenannten inversen Koeffizienten angeben. Sie zeigen letztlich wie Multiplikatoren die Gesamteffekte auf und betonen gleichzeitig die möglicherweise sehr unterschiedlichen Wirkungen auf die einzelnen Produktionsbereiche der Volkswirtschaft. Dies sind Informationen, die auch für die Wirtschaftspolitik relevant sind. Wenn z. B. in einer Rezession gefragt wird, welche Güter der Staat bei Auflage eines Konjunkturprogramms nachfragen soll, um möglichst starke Arbeitsmarkteffekte zu bewirken, kann dies unter Zuhilfenahme der I. beantwortet werden.
Literatur
M. Frenkel/K. John/R. Fendel: Volkswirtschaftliche Gesamtrechnung, 82016 • StBA: Volkswirtschaftliche Gesamtrechnungen. Input-Output-Rechnung 2012 (Revision 2014), Fachserie 18, Reihe 2, 2016 • StBA: Input-Output-Rechnung im Überblick, 2010.
Empfohlene Zitierweise
M. Frenkel: Input-Output-Rechnung, Version 08.06.2022, 09:10 Uhr, in: Staatslexikon8 online, URL: https://www.staatslexikon-online.de/Lexikon/Input-Output-Rechnung (abgerufen: 24.11.2024)